本来打算写篇关于ConcurrentSkipListMap的推文的,不过写这篇推文之前,我觉得还是有必要专门写一篇关于跳表的文章,只要理解的跳表,再看ConcurrentSkipListMap会容易很多,所以这篇文章就来介绍介绍跳表(SkipList)。
简介
先贴一段百度关于跳表的简介:
跳表是一个随机化的数据结构,可以被看做二叉树的一个变种,它在性能上和红黑树,AVL树不相上下,但是跳表的原理非常简单,目前在Redis和LeveIDB中都有用到。
它采用随机技术决定链表中哪些节点应增加向前指针以及在该节点中应增加多少个指针。跳表结构的头节点需有足够的指针域,以满足可能构造最大级数的需要,而尾节点不需要指针域。
采用这种随机技术,跳表中的搜索、插入、删除操作的时间均为O(logn),然而,最坏情况下时间复杂性却变成O(n)。相比之下,在一个有序数组或链表中进行插入/删除操作的时间为O(n),最坏情况下为O(n)。
回顾
首先我们回顾下之前有涉及到的数据结构,HashMap就涉及到了哈希表(数组+链表)、红黑树。
有序数组:这种方式的存储结构,优点是支持数据的随机访问,并且可以采用二分查找算法降低查找操作的复杂度。缺点同样很明显,插入和删除数据时,为了保持元素的有序性,需要进行大量的移动数据的操作。
二叉查找树:如果需要一个既支持高效的二分查找算法,又能快速的进行插入和删除操作的数据结构,那首先就是二叉查找树莫属了。缺点是在某些极端情况下,二叉查找树有可能变成一个线性链表。
AVL树(平衡二叉树):基于二叉查找树的优点,对其缺点进行改进,引入了平衡的概念。根据平衡算法的不同,具体实现有AVL树/B树(B-Tree)/B+树(B+Tree)/红黑树 等等。但是平衡二叉树的实现多数比较复杂,较难理解。
跳表核心思想
简介上也说了,它采用随机技术决定链表中哪些节点应增加向前指针以及在该节点中应增加多少个指针,所以跳表首先是一个有序的链表结构,链表结构相信大家再熟悉不过了,通过链表查询的时间复杂度很高,是O(n),这显然是比较慢了。而链表又没法进行二分搜索。了解了链表,跳表也很容易学。
我们先看下链表:
假如想要在其中查找某个数据,也只能从头到尾遍历链表,这样效率自然就会很低。比如想查询上图91这个数据,需要从6-14-29-43-55-64-72-91,遍历8个节点。
接着我们把该有序链表改造成跳表: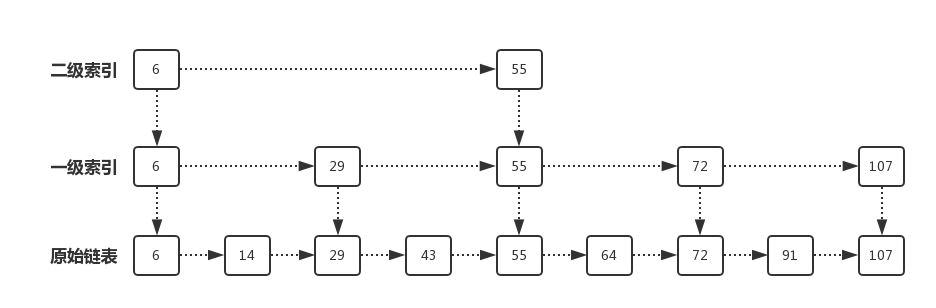
同样查询91,先从二级索引查,发现91大于55,就从55这个节点下移到一级索引,再在一级索引的55节点向后遍历,发现91位于72和107之间,然后从一级索引的72节点下移到原始链表的72节点,继续向后遍历,得到91,现在只需要遍历6个节点。
我们发现,加了索引后,查找一个结点需要遍历的次数减少了,也就是查找效率提高了。
当然现在模拟的数据较少,对比不怎么明显,加入数据多了,那么跳表的查找效率的提升就会非常明显。
这基本上就是跳表的核心思想,其实也是一种通过”空间来换取时间”的一个算法,通过在每个节点中增加了向前的指针,从而提升查找的效率。
贴一个gif给大家看下跳表插入节点的过程:
可见,跳表的时间复杂度为 O(logn),和二分查找、AVL的一样,但这其实是以空间来换时间的设计思路,在实际开发中,原始链表中存储的可能是很大的对象,而索引结点只需要存储关键值和几个指针,其额外占用的空间可以被忽略掉。
AVL实现也很复杂,但跳表的原理相当简单。
跳表性质
通过上述内容大家也大概知道跳表是个什么东西了,下面总结下跳表的性质(特性)
(1) 由很多层结构组成
(2) 每一层都是一个有序的链表
(3) 最底层(原始链表)的链表包含所有元素
(4) 如果一个元素出现在 Level n 的链表中,则它在 Level n 之下的链表也都会出现。
(5) 每个节点包含两个指针,一个指向同一链表中的下一个元素,一个指向下面一层的元素。
跳表的高度
之前的gif演示了如何在跳表插入一个元素,也很简单易懂,那么如何确定改元素的高度(层数)呢?
有趣的是,跳表里面元素的高度都是一种类似于随机的方法来确定,也叫抛硬币。。这也难怪简介里说跳表是一个随机化的数据结构了。。哈哈。

